1. 저항모멘트와 굽힘응력
하중을 받고 있는 보의 내부는 모든 단면이 굽힘모멘트를 받고 있다. 즉, 굽힘작용의 정도는 단면 편측의 힘의 모멘트 총합으로 나타내고, 이를 굽힘모멘트라 함.
이중 최대 굽힘모멘트와 이것이 발생하는 위치를 구하는 방법은 힘의 평형만을 생각하고, 어느 단면이라도 힘의 모멘트 합은 0이 되므로 평형상태가 된다.
그러나, 평형상태는 유지되지만, 단면의 위치 또는 보의 조건에 의해 달라진다.
인장이나 압축을 받는 기계 또는 구조물은 항상 안정한 상태에서 기능이 발휘되며, 외력에 의해 굽힘모멘트가 발생해도 파괴되지 않기 위해서는 평형상태를 유지하기 위한 저항이 재료내부에서 발생해야 한다.
그림과 같이 임의 단면 X에 굽힘모멘트 M이 발생하면, 보의 단면 X 오른쪽은 반시계방향의 M을 받으면서 파괴되지 않고 평형상태에 있는 것은 M과 크기가 같은 시계 방향의 모멘트 𝑀_𝑅 이 재료내부에 발생하기 때문이다.
𝑀_𝑅 은 M에 저항하여 발생한 모멘트이므로 저항모멘트라고 하며, 굽힘모멘트와 크기는 같으나, 방향은 반대이다.
굽힘모멘트는 보에 작용하는 하중에 의해 발생한 것으로 이미 배운 방법으로 크기를 계산할 수 있다.

저항모멘트는 굽힘작용 때문에 재료내부에 발생하는 응력에 의해 발생한 것으로, 저항모멘트를 계산하는 방법은 다음과 같다.
보가 굽힘모멘트 M을 받으면, AC측은 압축되고, BD측은 인장되어 ABCD는 A’B’C’D’와 같이 된다.
AC측은 압축응력, BD측은 인장응력이 발생되며, A’B’ 단면에는 반시계방향, C’D’단면에는 시계 방향의 저항모멘트가 발생한다. 이를 굽힘 때문에 보에 발생하는 응력이므로, 굽힘응력(bending stress)이라 한다.

ABCD면에서 중간층에는 압축 또는 인장이 없는 면, 즉 EF면은 중립면이라 한다.
중립면이 AB단면에 나타나는 직선 (그림(b)의 NN)을 중립축이라 한다. 이는 그 단면의 중심을 지나간다.
점 O에서 이루는 각을 𝜃라 하면, O에서 중립면 E’F’까지의 거리, 즉 중립면의 곡율반경을 𝜌이다. EF에서 임의거리 y 떨어진 층 GH가 굽힘에 의해 G’H’가 되었을 때의 변형률은
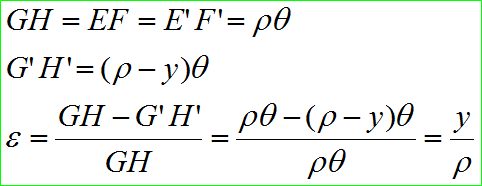
중립면에서 임의 거리 y에 있는 면의 변형률은 거리 y에 비례한다. 따라서 변형률과 동시에 발생하는 응력도 거리에 비례한다. 보 재료의 탄성계수를 E라고 하면, 최대응력은 거리 y가 최대인 A’C’에서 발생한다.
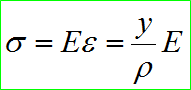
후크의 법칙이 성립하는 한도내에서는 순수굽힘에 의한 굽힘응력은 중립면으로부터 거리 y에 비례한다는 것을 알 수있다. (위의 식으로부터)
2. 단면계수
2.1 저항굽힘 모멘트
굽힘모멘트를 받는 보의 임의 단면에 발생하는 응력은 중립축의 거리에 비례한다. 응력의 분포를 그림에 나타냈다.

중립축 NN에서 임의거리 y에 있는 미소면적 ∆𝑎에 발생하는 응력을 𝜎이라 하면, 미소면적 ∆𝒂에 발생하는 전력 (all load)은 𝝈∆𝒂가 된다.
모든 힘이 NN을 축으로 하는 모멘트 ∆𝑀은
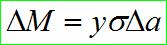
모멘트의 총합은

단면 2차 모멘트는
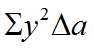
단면형상에 따라서 일정한 값을 가지며, 기호는 I로 나타낸다.
위의 식을 다시 고쳐쓰면, 다음과 같다.
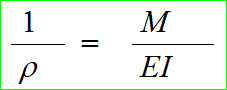
굽힘강성률계수 EI는 재료, 단면형상 및 치수에 따라서 일정하므로, 위의 식은 M이 크면, 𝜌는 작게 되고, M이 일정한 경우는 EI값이 클수록 𝜌는 크게 된다.
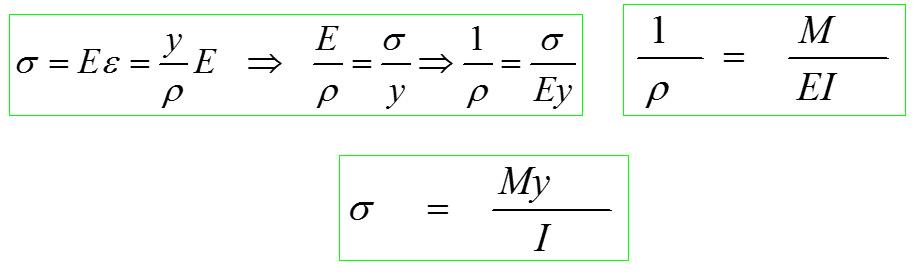
이 식은 굽힘응력이 중립면으로부터 가장 멀리 떨어진 면에서 최대값을 가지며, 아랫면에서 최대인장응력, 윗면에서 최대압축응력이 발생한다.
중립면에서 아랫면 및 윗면까지 거리를 각각 y𝑡, y𝑐 라 하면
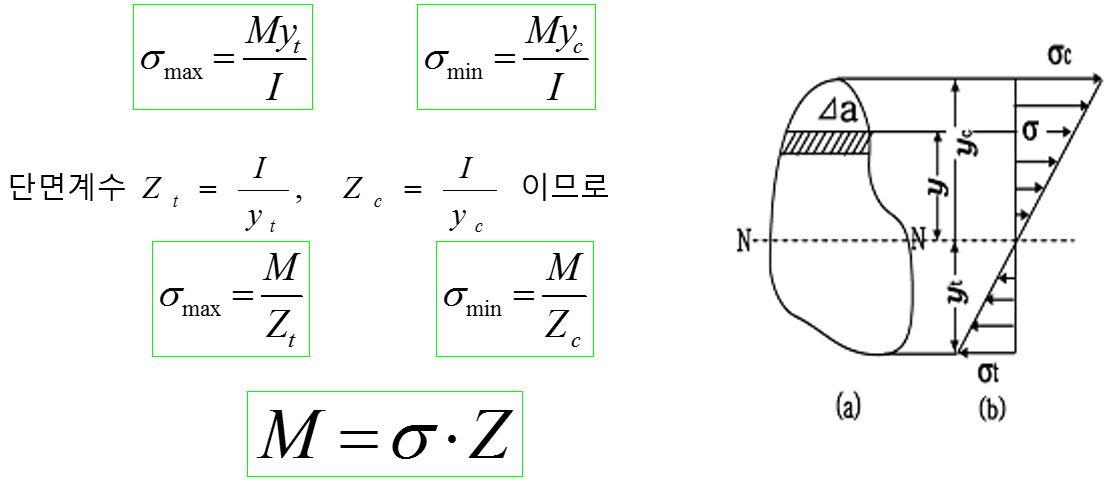
위의 식을 굽힘식 또는 저항굽힘모멘트라고 하며, 굽힘응력과 굽힘모멘트 사이의 관계식으로서 중요한 보의 설계 및 강도계산의 기초식으로 사용된다.
2.2 단면모멘트 (Ⅰ)
보에 발생하는 응력을 구하기 위해서는 단면의 도심을 구하고, 도심을 통과하는 중립축에 관한 단면 2차 모멘트를 계산해
야 한다.

그림과 같이 임의의 단면을 생각해서, 점 P(z, y)를 둘러싸는 미소면적 dA를 취한다. 미소면적와 임의의 축까지 거리와의 곱을 도형전체로 적분한 것을 단면 1차모멘트라 하다. 즉 Oz축, Oy축에 관한 1차 모멘트 Gz, Gy는 다음 식으로 주어진다.

단면의 면적을 A라 할 때, 좌표로 주어지는 점 G를 도심이라 한다.

만일 y, z 축의 한 축 또는 양축이 도심 G를 통과한다면, 한 축 또는 양축에 대한 각각의 단면 1차 모멘트는 윗식에서 Gy=0, Gz=0인 것을 알 수 있다.
그림의 미소단면 dA와 임의의 축까지 거리 제곱을 곱하여 도형전체에 대해 적분한 것을 단면 2차 모멘트라 한다. 즉 Oz축, Oy축에 관한 단면 2차 모멘트 Iz, Iy는 다음과 같다.
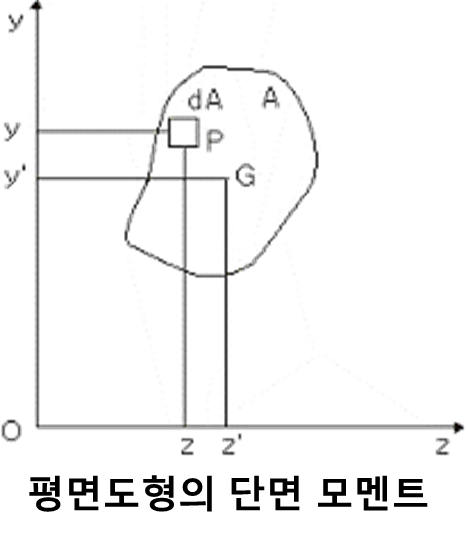

단면의 전면적이 어떤 점에 집중하고, 균일한 단면 2차 모멘트를 가지는 점을 취하여 축에서 그 점까지 거리를 단면 2차 반경이라 하고, 이를 Kz, Ky라 하면,
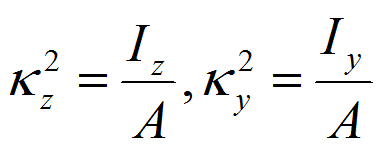
단면 2차 모멘트에는 몇 가지 중요한 정리가 있다. 그림과 같이 면적 A인 평면도형의 도심 G를 통과하는 z축에 관한 단면 2차모멘트 Iz와 이축에 평행하게 𝑙 거리 떨어진 𝑍_1 축에 관한 단면 2차 모멘트 I𝑧1 사이에는 다음관계가 성립한다. 미소면적 dA에서 z축까지 거리를 𝑦1이라 하면,
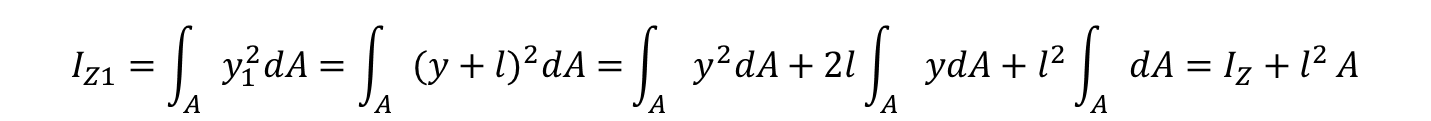
여기서, z축은 중립축과 일치하므로, 우변 2항은 0이 된다. 이 정리를 평행축 정리라 한다.

끝까지 읽어주셔서 감사합니다.
공감과 구독, 그리고 댓글은
저의 블로그 활동에
큰 원동력이 됩니다.
오늘도 좋은 하루 보내세요♥

[공학] 차량 중량, 축중 계산, 하중분포, 타이어 부하 등
차량 중량 1. 측정조건 (1) 자동차는 공차 또는 적차상태로 한다. (2) 공차상태의 중량분포로서 적차상태의 중량분포를 산출하기가 어려울 때에는 공차상태와 적차상태를 각각 측정한다. 이 경우
sugarlessgum.tistory.com
연성(Ductility) 취성(Brittle)
sugarlessgum.tistory.com
차량 용어 설명
*Ctrl + F : 검색 No.용 어정의 및 내용국문영문약어12륜구동 2 WHEEL DRIVE 2WD 2바퀴 굴림방식23D 항법장치 현행 Navigation System에 3차원 입체지도 표시 및 2화면 분활표시 등을 추가하고 실시간 교통정보
sugarlessgum.tistory.com




